FENÔMENOS DE TRANSPORTE
Calcular o volume de um reservatório, sabendo-se que a vazão de escoamento de um líquido é igual a 7 l/s. Para encher o reservatório totalmente são necessárias 2 horas e 15 minutos.
56,7 mm³
58,97 dm³
56,7 cm³
58,97 mm³
56,7 m³
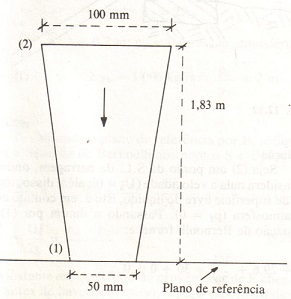
Considerar a água que escoa no sentido vertical descendente, em tubo tronco-cônico de 1,83 m de altura. As extremidades superior e inferior do tubo tem os diâmetros de 100 mm e 50 mm, respectivamente. Se a vazão é de 23 litros/s, achar a diferença de pressão entre as extremidades do tubo.
P1 - P2 = 4599,88 kgf / m²
P1 - P2 = 1000 kgf / m²
P1 - P2 = 6578 kgf / m²
P1 - P2 = 8899,23 kgf / m²
P1 - P2 = 10254,32 kgf / m²
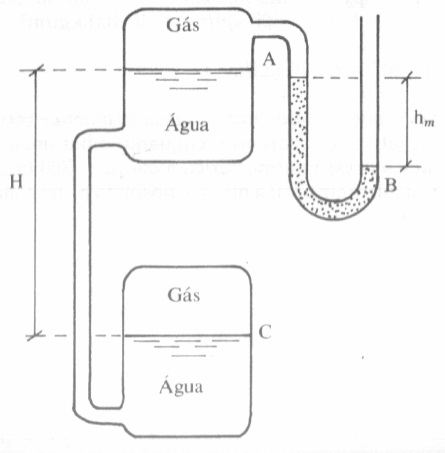
Estalos nos ouvidos é um fenômeno desconfortável experimentado quando ocorrem variações na pressão ambiente, por exemplo, em um elevador rápido, em um avião ou mesmo quando você está se dirigindo para o litoral onde você desce a serra. Se você está em um avião, a 3.000 m de altitude (massa específica do ar 0,909 kg/m³), e uma rápida descida de 100 m causa estalos em seus ouvidos, qual é a variação de pressão em milímetros de mercúrio (SGHg = 13,6) que causa este efeito? Se, em seguida, o avião sobe 8.000 m (massa específica do ar 0,526 kg/m³) e novamente começa a descer, quanto o avião descerá antes que seus ouvidos estalem novamente?
Altura de mercúrio - 15 m; altura em 8.000 m - 20 m.
Altura de mercúrio - 6,68 mm; altura em 8.000 m - 172,81 m.
Altura de mercúrio - 56 mm; altura em 8.000 m - 112 mm
Altura de mercúrio - 5,32 mm; altura em 8.000 m - 80 m.
Altura de mercúrio - 2,35 mm; altura em 8.000 m - 56,35 m.
Determine a densidade absoluta e o peso específico do ar nos sistemas de unidades (SI, MK*S) em condições normais (15 ºC e 101,3 kPa absolutos, Rar - 287 J/kg.K).
SI - 1,226 kg/m³; 12,03 N/m³;
MK*S - 0,125 UTM/m³; 1,227 kgf/m³;
SI - 0,86 kg/m³; 1,06 N/m³;
MK*S - 0,0235 UTM/m³; 2,325 kgf/m³;
SI - 1,226 kg/m³; 12,03 N/m³;
MK*S - 1,226 UTM/m³; 12,03 kgf/m³;
SI - 1,226 kg/m³; 12,03 N/m³;
MK*S - 1,226 UTM/m³; 1,227 kgf/m³;
SI - 10,25 kg/m³; 12,03 N/m³;
MK*S - 154 UTM/m³; 235 kgf/m³;
Um óleo de viscosidade dinâmica μ = 4.524×10-6 kgf⋅s/m² escoa, em regime laminar com velocidade igual a 1,08 m / s (velocidade central), num tubo de raio r = 90 mm. Supondo que o perfil de velocidades é linear, determinar:
I - O gradiente de velocidade (dv/dy);
II - A tensão de corte no fluido.
12 / s; 6,8 kgf / m²
15 s; 0,235 kgf / m²
12 / s; 3,2 kgf / m²
12 / s; 0,054 kgf / m²
12 / s; 0,054 N / m²
Um óleo de viscosidade absoluta 0,01 kgf.s/m² e densidade de 0,850 escoa através de 3000 m de um tubo de ferro fundido de 300 mm de diâmetro, à razão 50 l/s. Qual a perda de carga unitária no tubo? Considere g = 10 m / s²
3 m / m
0,003 m / m
0,03 m / m
300 m / m
30 m / m
Determine a potência de uma bomba em W e em CV com rendimento de 75%, pelo qual escoa água com uma vazão de 12 l/s. Dados: Hb = 20 m; massa especifica 1000 kg/m³; g = 10 m/s².
3200 W; 4,34 CV
700 W; 745 CV
56800 W; 23 CV
450 W; 1,23 CV
600 W; 10 CV
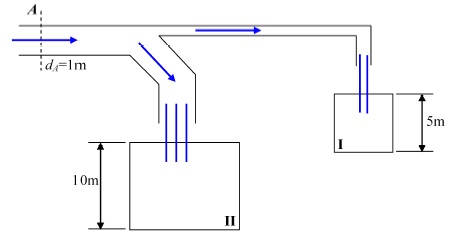
Os reservatórios I e II da figura abaixo são cúbicos. Eles são cheios pelas tubulações, respectivamente em 200 s e 1000 s. Determinar a velocidade da água na seção A indicada, sabendo-se que o diâmetro da tubulação é 1m. γ = 1000 Kg / m3.
4,56 m / s
1,07 m / s
0,58 m / s
2,07 m / s
54 m / s
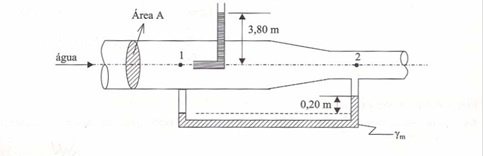
Dado o dispositivo da figura, calcular a vazão do escoamento da água no conduto. Desprezar as perdas e considerar o diagrama de velocidades uniforme. Dados: γH20 = 104 N/m³; γm = 6 X 104 N/m³; P2 = 20 kPa; A = 10-2 m²; g = 10 m/s².
56,7 mm³
58,97 dm³
56,7 cm³
58,97 mm³
56,7 m³
Considerar a água que escoa no sentido vertical descendente, em tubo tronco-cônico de 1,83 m de altura. As extremidades superior e inferior do tubo tem os diâmetros de 100 mm e 50 mm, respectivamente. Se a vazão é de 23 litros/s, achar a diferença de pressão entre as extremidades do tubo.

P1 - P2 = 4599,88 kgf / m²
P1 - P2 = 1000 kgf / m²
P1 - P2 = 6578 kgf / m²
P1 - P2 = 8899,23 kgf / m²
P1 - P2 = 10254,32 kgf / m²
Estalos nos ouvidos é um fenômeno desconfortável experimentado quando ocorrem variações na pressão ambiente, por exemplo, em um elevador rápido, em um avião ou mesmo quando você está se dirigindo para o litoral onde você desce a serra. Se você está em um avião, a 3.000 m de altitude (massa específica do ar 0,909 kg/m³), e uma rápida descida de 100 m causa estalos em seus ouvidos, qual é a variação de pressão em milímetros de mercúrio (SGHg = 13,6) que causa este efeito? Se, em seguida, o avião sobe 8.000 m (massa específica do ar 0,526 kg/m³) e novamente começa a descer, quanto o avião descerá antes que seus ouvidos estalem novamente?
Altura de mercúrio - 15 m; altura em 8.000 m - 20 m.
Altura de mercúrio - 6,68 mm; altura em 8.000 m - 172,81 m.
Altura de mercúrio - 56 mm; altura em 8.000 m - 112 mm
Altura de mercúrio - 5,32 mm; altura em 8.000 m - 80 m.
Altura de mercúrio - 2,35 mm; altura em 8.000 m - 56,35 m.
Determine a densidade absoluta e o peso específico do ar nos sistemas de unidades (SI, MK*S) em condições normais (15 ºC e 101,3 kPa absolutos, Rar - 287 J/kg.K).
SI - 1,226 kg/m³; 12,03 N/m³;
MK*S - 0,125 UTM/m³; 1,227 kgf/m³;
SI - 0,86 kg/m³; 1,06 N/m³;
MK*S - 0,0235 UTM/m³; 2,325 kgf/m³;
SI - 1,226 kg/m³; 12,03 N/m³;
MK*S - 1,226 UTM/m³; 12,03 kgf/m³;
SI - 1,226 kg/m³; 12,03 N/m³;
MK*S - 1,226 UTM/m³; 1,227 kgf/m³;
SI - 10,25 kg/m³; 12,03 N/m³;
MK*S - 154 UTM/m³; 235 kgf/m³;
Um óleo de viscosidade dinâmica μ = 4.524×10-6 kgf⋅s/m² escoa, em regime laminar com velocidade igual a 1,08 m / s (velocidade central), num tubo de raio r = 90 mm. Supondo que o perfil de velocidades é linear, determinar:
I - O gradiente de velocidade (dv/dy);
II - A tensão de corte no fluido.
12 / s; 6,8 kgf / m²
15 s; 0,235 kgf / m²
12 / s; 3,2 kgf / m²
12 / s; 0,054 kgf / m²
12 / s; 0,054 N / m²
Um óleo de viscosidade absoluta 0,01 kgf.s/m² e densidade de 0,850 escoa através de 3000 m de um tubo de ferro fundido de 300 mm de diâmetro, à razão 50 l/s. Qual a perda de carga unitária no tubo? Considere g = 10 m / s²
3 m / m
0,003 m / m
0,03 m / m
300 m / m
30 m / m
Determine a potência de uma bomba em W e em CV com rendimento de 75%, pelo qual escoa água com uma vazão de 12 l/s. Dados: Hb = 20 m; massa especifica 1000 kg/m³; g = 10 m/s².
3200 W; 4,34 CV
700 W; 745 CV
56800 W; 23 CV
450 W; 1,23 CV
600 W; 10 CV
Os reservatórios I e II da figura abaixo são cúbicos. Eles são cheios pelas tubulações, respectivamente em 200 s e 1000 s. Determinar a velocidade da água na seção A indicada, sabendo-se que o diâmetro da tubulação é 1m. γ = 1000 Kg / m3.

4,56 m / s
1,07 m / s
0,58 m / s
2,07 m / s
54 m / s
Dado o dispositivo da figura, calcular a vazão do escoamento da água no conduto. Desprezar as perdas e considerar o diagrama de velocidades uniforme. Dados: γH20 = 104 N/m³; γm = 6 X 104 N/m³; P2 = 20 kPa; A = 10-2 m²; g = 10 m/s².


P1 - P2 = 4599,88 kgf / m²
P1 - P2 = 1000 kgf / m²
P1 - P2 = 6578 kgf / m²
P1 - P2 = 8899,23 kgf / m²
P1 - P2 = 10254,32 kgf / m²
Estalos nos ouvidos é um fenômeno desconfortável experimentado quando ocorrem variações na pressão ambiente, por exemplo, em um elevador rápido, em um avião ou mesmo quando você está se dirigindo para o litoral onde você desce a serra. Se você está em um avião, a 3.000 m de altitude (massa específica do ar 0,909 kg/m³), e uma rápida descida de 100 m causa estalos em seus ouvidos, qual é a variação de pressão em milímetros de mercúrio (SGHg = 13,6) que causa este efeito? Se, em seguida, o avião sobe 8.000 m (massa específica do ar 0,526 kg/m³) e novamente começa a descer, quanto o avião descerá antes que seus ouvidos estalem novamente?
Altura de mercúrio - 15 m; altura em 8.000 m - 20 m.
Altura de mercúrio - 6,68 mm; altura em 8.000 m - 172,81 m.
Altura de mercúrio - 56 mm; altura em 8.000 m - 112 mm
Altura de mercúrio - 5,32 mm; altura em 8.000 m - 80 m.
Altura de mercúrio - 2,35 mm; altura em 8.000 m - 56,35 m.
Determine a densidade absoluta e o peso específico do ar nos sistemas de unidades (SI, MK*S) em condições normais (15 ºC e 101,3 kPa absolutos, Rar - 287 J/kg.K).
SI - 1,226 kg/m³; 12,03 N/m³;
MK*S - 0,125 UTM/m³; 1,227 kgf/m³;
SI - 0,86 kg/m³; 1,06 N/m³;
MK*S - 0,0235 UTM/m³; 2,325 kgf/m³;
SI - 1,226 kg/m³; 12,03 N/m³;
MK*S - 1,226 UTM/m³; 12,03 kgf/m³;
SI - 1,226 kg/m³; 12,03 N/m³;
MK*S - 1,226 UTM/m³; 1,227 kgf/m³;
SI - 10,25 kg/m³; 12,03 N/m³;
MK*S - 154 UTM/m³; 235 kgf/m³;
Um óleo de viscosidade dinâmica μ = 4.524×10-6 kgf⋅s/m² escoa, em regime laminar com velocidade igual a 1,08 m / s (velocidade central), num tubo de raio r = 90 mm. Supondo que o perfil de velocidades é linear, determinar:
I - O gradiente de velocidade (dv/dy);
II - A tensão de corte no fluido.
12 / s; 6,8 kgf / m²
15 s; 0,235 kgf / m²
12 / s; 3,2 kgf / m²
12 / s; 0,054 kgf / m²
12 / s; 0,054 N / m²
Um óleo de viscosidade absoluta 0,01 kgf.s/m² e densidade de 0,850 escoa através de 3000 m de um tubo de ferro fundido de 300 mm de diâmetro, à razão 50 l/s. Qual a perda de carga unitária no tubo? Considere g = 10 m / s²
3 m / m
0,003 m / m
0,03 m / m
300 m / m
30 m / m
Determine a potência de uma bomba em W e em CV com rendimento de 75%, pelo qual escoa água com uma vazão de 12 l/s. Dados: Hb = 20 m; massa especifica 1000 kg/m³; g = 10 m/s².
3200 W; 4,34 CV
700 W; 745 CV
56800 W; 23 CV
450 W; 1,23 CV
600 W; 10 CV
Os reservatórios I e II da figura abaixo são cúbicos. Eles são cheios pelas tubulações, respectivamente em 200 s e 1000 s. Determinar a velocidade da água na seção A indicada, sabendo-se que o diâmetro da tubulação é 1m. γ = 1000 Kg / m3.

4,56 m / s
1,07 m / s
0,58 m / s
2,07 m / s
54 m / s
Dado o dispositivo da figura, calcular a vazão do escoamento da água no conduto. Desprezar as perdas e considerar o diagrama de velocidades uniforme. Dados: γH20 = 104 N/m³; γm = 6 X 104 N/m³; P2 = 20 kPa; A = 10-2 m²; g = 10 m/s².

Altura de mercúrio - 15 m; altura em 8.000 m - 20 m.
Altura de mercúrio - 6,68 mm; altura em 8.000 m - 172,81 m.
Altura de mercúrio - 56 mm; altura em 8.000 m - 112 mm
Altura de mercúrio - 5,32 mm; altura em 8.000 m - 80 m.
Altura de mercúrio - 2,35 mm; altura em 8.000 m - 56,35 m.
Determine a densidade absoluta e o peso específico do ar nos sistemas de unidades (SI, MK*S) em condições normais (15 ºC e 101,3 kPa absolutos, Rar - 287 J/kg.K).
SI - 1,226 kg/m³; 12,03 N/m³;
MK*S - 0,125 UTM/m³; 1,227 kgf/m³;
SI - 0,86 kg/m³; 1,06 N/m³;
MK*S - 0,0235 UTM/m³; 2,325 kgf/m³;
SI - 1,226 kg/m³; 12,03 N/m³;
MK*S - 1,226 UTM/m³; 12,03 kgf/m³;
SI - 1,226 kg/m³; 12,03 N/m³;
MK*S - 1,226 UTM/m³; 1,227 kgf/m³;
SI - 10,25 kg/m³; 12,03 N/m³;
MK*S - 154 UTM/m³; 235 kgf/m³;
Um óleo de viscosidade dinâmica μ = 4.524×10-6 kgf⋅s/m² escoa, em regime laminar com velocidade igual a 1,08 m / s (velocidade central), num tubo de raio r = 90 mm. Supondo que o perfil de velocidades é linear, determinar:
I - O gradiente de velocidade (dv/dy);
II - A tensão de corte no fluido.
12 / s; 6,8 kgf / m²
15 s; 0,235 kgf / m²
12 / s; 3,2 kgf / m²
12 / s; 0,054 kgf / m²
12 / s; 0,054 N / m²
Um óleo de viscosidade absoluta 0,01 kgf.s/m² e densidade de 0,850 escoa através de 3000 m de um tubo de ferro fundido de 300 mm de diâmetro, à razão 50 l/s. Qual a perda de carga unitária no tubo? Considere g = 10 m / s²
3 m / m
0,003 m / m
0,03 m / m
300 m / m
30 m / m
Determine a potência de uma bomba em W e em CV com rendimento de 75%, pelo qual escoa água com uma vazão de 12 l/s. Dados: Hb = 20 m; massa especifica 1000 kg/m³; g = 10 m/s².
3200 W; 4,34 CV
700 W; 745 CV
56800 W; 23 CV
450 W; 1,23 CV
600 W; 10 CV
Os reservatórios I e II da figura abaixo são cúbicos. Eles são cheios pelas tubulações, respectivamente em 200 s e 1000 s. Determinar a velocidade da água na seção A indicada, sabendo-se que o diâmetro da tubulação é 1m. γ = 1000 Kg / m3.

4,56 m / s
1,07 m / s
0,58 m / s
2,07 m / s
54 m / s
Dado o dispositivo da figura, calcular a vazão do escoamento da água no conduto. Desprezar as perdas e considerar o diagrama de velocidades uniforme. Dados: γH20 = 104 N/m³; γm = 6 X 104 N/m³; P2 = 20 kPa; A = 10-2 m²; g = 10 m/s².

SI - 1,226 kg/m³; 12,03 N/m³;
MK*S - 0,125 UTM/m³; 1,227 kgf/m³;
SI - 0,86 kg/m³; 1,06 N/m³;
MK*S - 0,0235 UTM/m³; 2,325 kgf/m³;
SI - 1,226 kg/m³; 12,03 N/m³;
MK*S - 1,226 UTM/m³; 12,03 kgf/m³;
SI - 1,226 kg/m³; 12,03 N/m³;
MK*S - 1,226 UTM/m³; 1,227 kgf/m³;
SI - 10,25 kg/m³; 12,03 N/m³;
MK*S - 154 UTM/m³; 235 kgf/m³;
Um óleo de viscosidade dinâmica μ = 4.524×10-6 kgf⋅s/m² escoa, em regime laminar com velocidade igual a 1,08 m / s (velocidade central), num tubo de raio r = 90 mm. Supondo que o perfil de velocidades é linear, determinar:
I - O gradiente de velocidade (dv/dy);
II - A tensão de corte no fluido.
12 / s; 6,8 kgf / m²
15 s; 0,235 kgf / m²
12 / s; 3,2 kgf / m²
12 / s; 0,054 kgf / m²
12 / s; 0,054 N / m²
Um óleo de viscosidade absoluta 0,01 kgf.s/m² e densidade de 0,850 escoa através de 3000 m de um tubo de ferro fundido de 300 mm de diâmetro, à razão 50 l/s. Qual a perda de carga unitária no tubo? Considere g = 10 m / s²
3 m / m
0,003 m / m
0,03 m / m
300 m / m
30 m / m
Determine a potência de uma bomba em W e em CV com rendimento de 75%, pelo qual escoa água com uma vazão de 12 l/s. Dados: Hb = 20 m; massa especifica 1000 kg/m³; g = 10 m/s².
3200 W; 4,34 CV
700 W; 745 CV
56800 W; 23 CV
450 W; 1,23 CV
600 W; 10 CV
Os reservatórios I e II da figura abaixo são cúbicos. Eles são cheios pelas tubulações, respectivamente em 200 s e 1000 s. Determinar a velocidade da água na seção A indicada, sabendo-se que o diâmetro da tubulação é 1m. γ = 1000 Kg / m3.

4,56 m / s
1,07 m / s
0,58 m / s
2,07 m / s
54 m / s
Dado o dispositivo da figura, calcular a vazão do escoamento da água no conduto. Desprezar as perdas e considerar o diagrama de velocidades uniforme. Dados: γH20 = 104 N/m³; γm = 6 X 104 N/m³; P2 = 20 kPa; A = 10-2 m²; g = 10 m/s².

12 / s; 6,8 kgf / m²
15 s; 0,235 kgf / m²
12 / s; 3,2 kgf / m²
12 / s; 0,054 kgf / m²
12 / s; 0,054 N / m²
Um óleo de viscosidade absoluta 0,01 kgf.s/m² e densidade de 0,850 escoa através de 3000 m de um tubo de ferro fundido de 300 mm de diâmetro, à razão 50 l/s. Qual a perda de carga unitária no tubo? Considere g = 10 m / s²
3 m / m
0,003 m / m
0,03 m / m
300 m / m
30 m / m
Determine a potência de uma bomba em W e em CV com rendimento de 75%, pelo qual escoa água com uma vazão de 12 l/s. Dados: Hb = 20 m; massa especifica 1000 kg/m³; g = 10 m/s².
3200 W; 4,34 CV
700 W; 745 CV
56800 W; 23 CV
450 W; 1,23 CV
600 W; 10 CV
Os reservatórios I e II da figura abaixo são cúbicos. Eles são cheios pelas tubulações, respectivamente em 200 s e 1000 s. Determinar a velocidade da água na seção A indicada, sabendo-se que o diâmetro da tubulação é 1m. γ = 1000 Kg / m3.

4,56 m / s
1,07 m / s
0,58 m / s
2,07 m / s
54 m / s
Dado o dispositivo da figura, calcular a vazão do escoamento da água no conduto. Desprezar as perdas e considerar o diagrama de velocidades uniforme. Dados: γH20 = 104 N/m³; γm = 6 X 104 N/m³; P2 = 20 kPa; A = 10-2 m²; g = 10 m/s².

3 m / m
0,003 m / m
0,03 m / m
300 m / m
30 m / m
Determine a potência de uma bomba em W e em CV com rendimento de 75%, pelo qual escoa água com uma vazão de 12 l/s. Dados: Hb = 20 m; massa especifica 1000 kg/m³; g = 10 m/s².
3200 W; 4,34 CV
700 W; 745 CV
56800 W; 23 CV
450 W; 1,23 CV
600 W; 10 CV
Os reservatórios I e II da figura abaixo são cúbicos. Eles são cheios pelas tubulações, respectivamente em 200 s e 1000 s. Determinar a velocidade da água na seção A indicada, sabendo-se que o diâmetro da tubulação é 1m. γ = 1000 Kg / m3.

4,56 m / s
1,07 m / s
0,58 m / s
2,07 m / s
54 m / s
Dado o dispositivo da figura, calcular a vazão do escoamento da água no conduto. Desprezar as perdas e considerar o diagrama de velocidades uniforme. Dados: γH20 = 104 N/m³; γm = 6 X 104 N/m³; P2 = 20 kPa; A = 10-2 m²; g = 10 m/s².

3200 W; 4,34 CV
700 W; 745 CV
56800 W; 23 CV
450 W; 1,23 CV
600 W; 10 CV
Os reservatórios I e II da figura abaixo são cúbicos. Eles são cheios pelas tubulações, respectivamente em 200 s e 1000 s. Determinar a velocidade da água na seção A indicada, sabendo-se que o diâmetro da tubulação é 1m. γ = 1000 Kg / m3.

4,56 m / s
1,07 m / s
0,58 m / s
2,07 m / s
54 m / s
Dado o dispositivo da figura, calcular a vazão do escoamento da água no conduto. Desprezar as perdas e considerar o diagrama de velocidades uniforme. Dados: γH20 = 104 N/m³; γm = 6 X 104 N/m³; P2 = 20 kPa; A = 10-2 m²; g = 10 m/s².


4,56 m / s
1,07 m / s
0,58 m / s
2,07 m / s
54 m / s
Dado o dispositivo da figura, calcular a vazão do escoamento da água no conduto. Desprezar as perdas e considerar o diagrama de velocidades uniforme. Dados: γH20 = 104 N/m³; γm = 6 X 104 N/m³; P2 = 20 kPa; A = 10-2 m²; g = 10 m/s².